|
|
2.2.The new algorithm: a fully on-line modification of the E-method
In the previous
section it was noticed that a full precision representation of the elements
of the matrix
and the right-hand side vector
is needed in order to initiate the computations. However the result
is generated in an on-line manner, i.e. the equally positioned digits of all
the components of the solution vector are produced simultaneously at each iteration
step starting from the most significant digit at the first iteration step and
proceeding with the less significant digits as the iteration index increases.
Next we shall
propose a new fully on-line algorithm in which the elements of the matrix
and the right-hand side vectorare involved into computation serially digit-by-digit
starting from the most significant digits in exactly the same way the result
digits in the original E-method are generated. The recurrence equations of this
new fully on-line algorithm for solving linear systems of algebraic equations
can be derived in a way similar to the one we used in the previous section.
First we shall introduce some new values related to the coefficient matrixand the right-hand side vector
in addition to those described already above:
is the on-line representation of the i-th component of
the right-hand side vector with all the digits 
belonging to the redundant digit set {-1, 0, 1} and d is the
on-line delay;
is the on-line representation of the right-hand side vector;
is the vector of the j-th most significant digits of the
right-hand side components 
, i=1, 2, ...., n;
From the last definitions we can obtain immediately the result:
(9)
and
.
We proceed with our last three definitions:
is the on-line representation of the coefficient
with all the digits
belonging to the redundant digit set {-1, 0, 1};
is the on-line representation of the coefficient
matrix;
is the matrix of the j-th most significant digits of the
coefficients , i= 1, 2, ... , n.
Again we have an immediate result from the last definitions:
(10) 
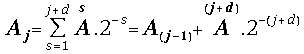and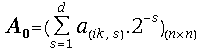 
.
Our next step
is to define residual vectors 
:
(11) 
We suppose now
that there exists a selection rule 
as described by (4), such that if
,then 
. Obviously 
and 
. So we have 
and 
is the solution of the system (1). From (2), (9) and (10) a recurrence
equation for the residual vectors
can be derived as follows:
(12) 
=
=
=
=
=
=
=
;
,
, j = 0, 1, 2, ....
From (12) for
the scaled residual vectors 
we finally obtain:
(13)
;
, j = 0, 1, 2, ....
Our last step
is to specify a selection rule
of the type (8). We choose for this purpose the standard radix-2
SRT-division selection rule. Namely:
(14) 
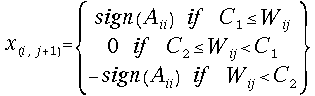for all i, j;
where
and
are the comparison constants. Supposing for definiteness that the
equations of the system are scaled so that 
(exceeding unity but being very close to it) for all 
the preferred choice usually is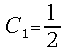
and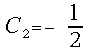
, so the selection rule can easily be modified into a rounding procedure.
We must note that it is possible to have individual pairs of comparison constants
and
for each value of i in the
general case, but this is irrelevant to our discussion. Evidently the structure
of the new fully on-line method is similar to the structure of the original
E-method. However the scalar recurrences are considerably more complex according
to (13). It is also possible to use truncated versions of the scaled residuals
in the selection rule, but these versions
must contain larger number of digits in comparison with the original E-method.
